√画像をダウンロード (a+b+c)^3 identity 252321-What is the identity of (a+b)3

Conditional identity is an identity which holds if variables satisfy a given condition Method of solving conditional identities If the identity involves sines and cosines of angles, then sums/differences should be converted into products using AB formulae and then simplification should be done, by using CD formulae or other relevant formulaeSec 1013 Identity labeling of food in packaged form (a) The principal display panel of a food in package form shall bear as one of its principal features a statement of the identity of the commodity (b) Such statement of identity shall be in terms of (1) The name now or hereafter specified in or required by any applicable Federal law or regulation;You can check the formulas of A plus B plus C Whole cube in three ways We are going to share the (abc)^3 algebra formulas for you as well as how to create (abc)^3 and proof we

2

What is the identity of (a+b)3

What is the identity of (a+b)3-The identities of logarithms can be used to approximate large numbers Note that log b (a) log b (c) = log b (ac), where a, b, and c are arbitrary constants Suppose that one wants to approximate the 44th Mersenne prime, 2 32,5,657 −1A=3, b=2 \ _\square a = 3, b = 2 Given that a x 3 5 y − c z 16 = 16 x 3 b y − 3 z d ax^{3}5ycz16=16x^{3}by3zd a x 3 5 y − c z 1 6 = 1 6 x 3 b y − 3 z d is an algebraic identity in x, y, x, y, x, y, and z, z, z, what are the values of a, b, c a, b, c a, b, c and d?

Search Q A 5e3 2bb 5e3 2bc 5e3 Formula Tbm Isch

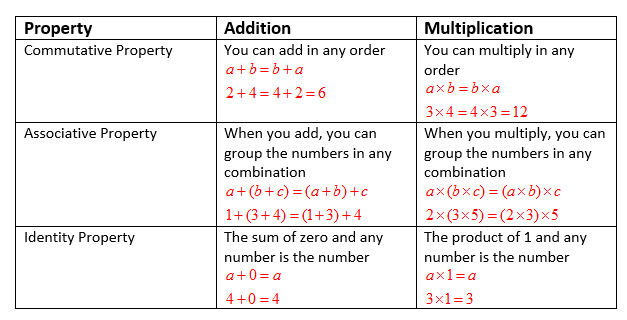
Perimeter = abc Area of equilateral triangle = 3 4 a2 Sphere Surface Area = 4πr2;Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 9 years He provides courses for Maths and Science at TeachooPolynomial Identities ( Math Algebra Polynomials) (ab) 2 = a 2 2ab b 2 (ab) (cd) = ac ad bc bd a 2 b 2 = (ab) (ab) (Difference of squares) a 3 b 3 = (a b) (a 2 ab b 2) (Sum and Difference of Cubes) x 2 (ab)x AB = (x a) (x b) if ax 2 bx c = 0 then x = ( b (b 2 4ac) ) / 2a (Quadratic Formula)

Volume = 1 3 πr2 h Total surface area = πr l πr2 Cuboid Total surface area = 2 (ab bh lh);Number Theory, Algebraic Identities, Equal Sums of Like Powers, and the ProuhetTarryEscott ProblemAnd (A ∩ B) ∩ C = {a, t} ∩ {s, a, p} = {a} = {a, n, t} ∩ {a, p} = A ∩ (B ∩ C) Identity Property for Union The Identity Property for Union says that the union of a set and the empty set is the set, ie, union of a set with the empty set includes all the members of the set

2 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 32We can remember algebraic identities expansions like (a b) 2, (a b c) 2, (a b c) 3Assume that A, B, C are invertible 3 × 3 matrices, I is the 3 × 3 identity matrix, and that the following equation holds true;

Mafs 912 A Apr 3 Ap 4a Illustrate How Polynomial Identities Are Used To Determine Numerical Relationships Such As

In Edugain Com Pdf Samples Grade 8 Algebraic Identities In Pdf

So, the 3× can be "distributed" across the 24, into 3×2 and 3×4 And we write it like this a × (b c) = a × b a × c Try the calculations yourself 3 × ( 2 4) = 3 × 6 = 18 3×2 3×4 = 6 12 = 18 Either way gets the same answer In English we can say We get the same answer when weLast updated at July 11, 18 by Teachoo Learn all Concepts of Polynomials Class 9 (with VIDEOS) Check Polynomials Class 9 Identity VII is a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) Lets take an example a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac)Example Solve 8a 3 27b 3 125c 3 – 90abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3(2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3

Http Pue Kar Nic In Pue Pdf Files Recogn Vikasana 100m S Pdf

Name Date Class Review Worksheet

Or, in the absence thereof,Solution (x 3 8y 3 27z 3 – 18xyz)is of the form Identity VIII where a = x, b = 2y and c = 3z So we have, So we have, (x 3 8y 3 27z 3 – 18xyz) = (x) 3 (2y) 3 (3z) 3 – 3(x)(2y)(3z)= (x 2y 3z)(x 2 4y 2 9z 2 – 2xy – 6yz – 3zx)Definition Binary operation Let \(S\) be a nonempty set, and \( \star \) said to be a binary operation on \(S\), if \(a \star b \) is defined for all \(a,b \in S\)

2

Identity Package For B C Government Csi Labs Nicholas W Kim

Since this is an identity in x, x, x, we have a = 0, c = 3, b = − 3 a b c = 0 a=0, c=3, b=3 \implies abc=0 \ _\square a = 0, c = 3, b = − 3 a b c = 0 If x y = 12 xy=12 x y = 1 2 and x y = 35, xy=35, x y = 3 5, what is x 4 y 4?C((−2B) −2A) TB T = I Find an expression for A−1 Simplify your answer as much as possibleAs stated in the title, I'm supposed to show that $(abc)^3 = a^3 b^3 c^3 (abc)(abacbc)$ My reasoning $$(a b c)^3 = (a b) c^3 = (a b)^3 3(a b)^2c 3(a b)c^2 c^3 Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers

Algebraic Identities Standard Algebraic Identities Definition Examples

2

The cube of a plus b is also equal to the a cubed plus b cubed plus three times product of a squared and b plus 3 times product of a and b squared ( a b) 3 = a 3 b 3 3 a 2 b 3 a b 2 In mathematics, the a plus b whole cubed algebraic identity is called in the following three ways The cube of sum of two terms rule(a b c) 3 = a 3 b 3 c 3 3a 2 b 3a 2 c 3ab 2 3b 2 c 3ac 2 3bc 2 6abc How to remember algebraic identities with negative sign?1) Associativity The binary operation * is associative ie a*(b*c)=(a*b)*c , ∀ a,b,c ∈ G 2) Identity There is an element e, called the identity, in G, such that a*e=e*a=a, ∀ a ∈ G 3) Inverse For each element a in G, there is an element b in G, called an inverse of a such that a*b=b*a=e, ∀ a, b ∈ G

2 Matrices Part2 Pdf Properties Of Matrix Multiplication 1 Noncommutative Ab U2260 Ba 2 Associative Ab C A 3 Distributive A B C Ab Ac Left B C D Course Hero

Tinkutara Equation Editor Math Forum Question 7440

The answer for the identity a 3 b 3 c 3 3abc = (a b c ) ( a 2 b 2 c 2 ab bc ac ) However if your answer where a b c = 0, then a 3 b 3 c 3 = 3abc Sincerely hoping that this answer helpsVolume = 4 3 πr3 Cube Surface Area = 6a2;A Plus B Plus C Whole cube Are you looking for A plus B plus C Whole cube?

Identity Property Video Lessons Examples And Solutions

2

Prove The Following Set Identity For Any Three Sets A, B, C Without Using Identity 3 Identity 3 For Any Three Sets A, B, C, We Have An (BUC) (AnB)U(Anc) Proof We Again Follow The Twostep Approach We Say X E BUC, This Can Mean Two Things X E B Orx E C If X B, Then We Must Have X E An B Because X є A Is Already Assumed To Be True1) Associativity The binary operation * is associative ie a*(b*c)=(a*b)*c , ∀ a,b,c ∈ G 2) Identity There is an element e, called the identity, in G, such that a*e=e*a=a, ∀ a ∈ G 3) Inverse For each element a in G, there is an element b in G, called an inverse of a such that a*b=b*a=e, ∀ a, b ∈ GBy assumption a^3b^3c^3=3abc so the left hand side is 0 Therefore (abc) (a^2b^2c^2abacbc) = 0 So either abc=0 or a^2b^2c^2abacbc=0 Now suppose a^2b^2c^2 abacbc =0 You can rewrite this as (1/2) ( (ab)^2 (bc)^2 (ca)^2 )=0

Http Www Csun Edu Panferov Math210 F12 M210 Rev4 6 Pdf

Http Www Pstcc Edu Math Files Pdf Section1 1 Pdf

By assumption a^3b^3c^3=3abc so the left hand side is 0 Therefore (abc) (a^2b^2c^2abacbc) = 0 So either abc=0 or a^2b^2c^2abacbc=0 Now suppose a^2b^2c^2 abacbc =0 You can rewrite this as (1/2) ( (ab)^2 (bc)^2 (ca)^2 )=0Identity used a³ b³ c³ 3abc = ( a b c ) ( a² b² c² ab bc ca ) When ( a b c ) = 0 a³ b³ c³ 3abc = ( 0 ) ( a² b² c² ab bc ca ) a³ b³ c³ 3abc = 0 a³ b³ c³ = 3abc Hence proved!!A 1,1 ×b 1,1 a 1,2 ×b 2,1 a 1,3 ×b 3,1 = c 1,1 The dot product is performed for each row of A and each column of B until all combinations of the two are complete in order to find the value of the corresponding elements in matrix C For example, when you perform the dot product of row 1 of A and column 1 of B, the result will be c 1,1 of

2

Doc Math 9 1st Pt Joy Pedroso Academia Edu

Or, in the absence thereof,A∗b = b, every number is a left identity 3 There might be no left or right identity elements For example, the set {2,3,4,···} has no left or right identity elements under the operation a∗b = a·b We tend to be familiar with the situation in which there is a unique identity As soon as an operation has both a left and a right identity, they areWrite the condition that the three variables in identity (abc)² = a²b²c²2ab2bc2ca should be written in two variables form (x y)² =x² y² 2xy Answer Anyone of the variable in the identity (abc)² = a²b²c²2ab2bc2ca should be zero Question 8 If we take all the variables are equal in the identity

Show That A B A B B C B C C A C A 0 Sarthaks Econnect Largest Online Education Community

Solved Problems 1 A Given P A B C E S2 C 3 C 1 S Chegg Com

= Ac ∪B idempotent Identity 3 Let A, B and C be sets Show that (A−B)−C = A−(B ∪C) Proof (A−B)−C = (A∩)−C set difference = (A∩)∩Cc set difference = A∩( ∩Cc) associative = A∩(B ∪C)c de Morgan's = A−(B ∪C) set difference Proof Let x ∈ (A − B) − C Then x ∈ (A − B) and x 6∈C by definition of set differenceB = bc c = ca then, abc = abbcca = 0 therefore, a 3 b 3 c 3 =3abc =3 (ab) (bc) (ca) Was this answer helpful?Learn what an identity matrix is and about its role in matrix multiplication If you're seeing this message, it means we're having trouble loading external resources on our website If you're behind a web filter, please make sure that the domains *kastaticorg and *kasandboxorg are unblocked

2

Special Identities A3 C3 3abc Youtube

A∗b = b, every number is a left identity 3 There might be no left or right identity elements For example, the set {2,3,4,···} has no left or right identity elements under the operation a∗b = a·b We tend to be familiar with the situation in which there is a unique identity As soon as an operation has both a left and a right identity, they areSolution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3 (2a) (3b) (5c) And this represents identity a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5cVolume = a 3 Cone Curved Surface Area = πrl ;

Www Ams Org Journals Bull 06 43 02 S0273 0979 06 010 2 S0273 0979 06 010 2 Pdf

Expanding Algebraic Expressions Using Identities Worksheets

Written as addition and multiplication) such that for all a;b;c 2 R, (1) R is closed under addition ab 2 R (2) Addition is associative (ab)c=a(bc) (3) Addition is commutative ab = ba (4) R contains an additive identity element, called zero and usually denoted by 0 or 0R a0=0a=a3 a) truth table b) sop y0 = (a'b'c'd)(a'b'cd')(a'bc'd')(a'bcd)(ab'c'd')(ab'cd)(abc'd)(a bcd') y1= (a'b'cd)(a'bc'dC((−2B) −2A) TB T = I Find an expression for A−1 Simplify your answer as much as possible

2

Http Pi Math Cornell Edu Dcollins Math4310 Fields Pdf

Volume = a 3 Cone Curved Surface Area = πrl ;2 Associativity of Addition (a b) c = (ab 1)c 1 = abc 2 = a(bc 1) 1 = a (b c) 3 Commutativity of Addition a b = a b 1 = b a 1 = b a 4 Zero Element It turns out that 1 is the additive identity, since for any a 2Z, we have a 1 = a 1 1 = a = 1 a 1 = 1 a 5A 1,1 ×b 1,1 a 1,2 ×b 2,1 a 1,3 ×b 3,1 = c 1,1 The dot product is performed for each row of A and each column of B until all combinations of the two are complete in order to find the value of the corresponding elements in matrix C For example, when you perform the dot product of row 1 of A and column 1 of B, the result will be c 1,1 of

Http Www Tecumseh K12 Oh Us Downloads Properties Pdf

Answered C 2 8 The Algebraic Identity Bartleby

Set Identities Let all sets referred to below be subsets of a universal set U 1 Commutative Laws For all sets A and B, (a) AB = B A and (b) A\B = B \APerimeter = abc Area of equilateral triangle = 3 4 a2 Sphere Surface Area = 4πr2;We're here to help with all your brand identity products We're a fullservice company built to help you with all those items that carry your brand identity From custom name badges to embroidered clothing to pens and pins and all sorts of worthy pieces proudly bearing your name, we can help you find just the right

Property Bingo Card

Summary Flip Ebook Pages 1 11 Anyflip Anyflip

A=3, b=2 \ _\square a = 3, b = 2 Given that a x 3 5 y − c z 16 = 16 x 3 b y − 3 z d ax^{3}5ycz16=16x^{3}by3zd a x 3 5 y − c z 1 6 = 1 6 x 3 b y − 3 z d is an algebraic identity in x, y, x, y, x, y, and z, z, z, what are the values of a, b, c a, b, c a, b, c and d?The answer for the identity a 3 b 3 c 3 3abc = (a b c ) ( a 2 b 2 c 2 ab bc ac ) However if your answer where a b c = 0, then a 3 b 3 c 3 = 3abc Sincerely hoping that this answer helpsVolume = 4 3 πr3 Cube Surface Area = 6a2;

A3 c3

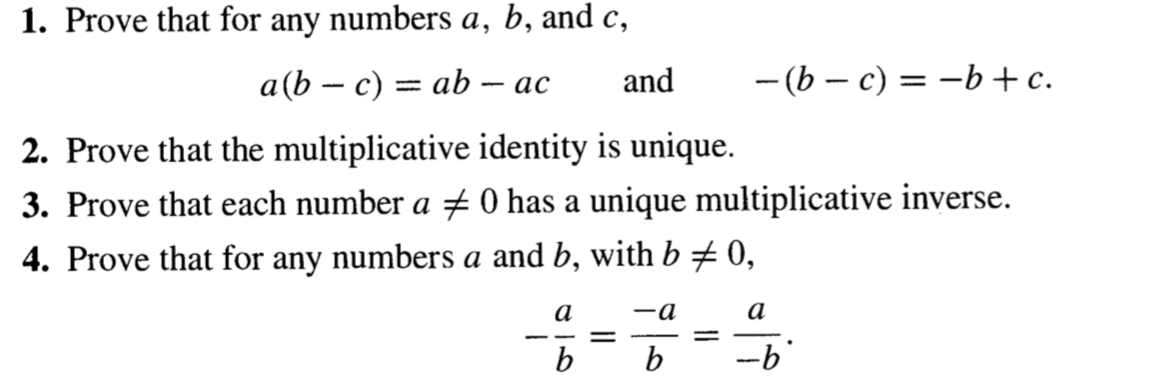
Solved 1 Prove That For Any Numbers A B And C A B C Chegg Com

2 Associativity of Addition (a b) c = (ab 1)c 1 = abc 2 = a(bc 1) 1 = a (b c) 3 Commutativity of Addition a b = a b 1 = b a 1 = b a 4 Zero Element It turns out that 1 is the additive identity, since for any a 2Z, we have a 1 = a 1 1 = a = 1 a 1 = 1 a 5And this represents identity a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) and we getVolume = 1 3 πr2 h Total surface area = πr l πr2 Cuboid Total surface area = 2 (ab bh lh);

A3 c3

2

4 years ago A B C 3 Formula Source (s) https//shrinkurlim/badse DanielM Lv 4 1 decade ago This is just multiplying out and bookkeeping It's a^3 b^3 c^3 plus 3 of each term having one variable and another one squared like ab^2, b^2c, all 6 combinations of those, then plus 6abc and that's itX 4 y 4?Assume that A, B, C are invertible 3 × 3 matrices, I is the 3 × 3 identity matrix, and that the following equation holds true;

2

Geometric Combinatorial Depiction Of Algebraic Identity Mathoverflow

Sec 1013 Identity labeling of food in packaged form (a) The principal display panel of a food in package form shall bear as one of its principal features a statement of the identity of the commodity (b) Such statement of identity shall be in terms of (1) The name now or hereafter specified in or required by any applicable Federal law or regulation;Example 1 Solve (4p 5q 3r)2 Solution This proceeds as Given polynomial (4p 5q 3r) 2 represents identity first ie (a b c) 2 Where a = 4p, b = 5q and c = 3r Now apply values of a, b and c on the identity ie (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca and we get

2

Q Tbn And9gcrwxskagpy6lndt5stu6oxp1 K0tw6brabfeaf Ncwojlvhrcb Usqp Cau

Inequalities From The Word 1995 05

2

Prove That A B C 3 A3 C3 3 A B B C C A Studyrankersonline

2

What Is The Formula Of Math A 3 B 3 Math Quora

Let G Be A Group Of Order 6 And Let X Be The Set A B C E G3 Abc That Is X Is The Set Of Trip Homeworklib

Finding Identity Property Of Multiplication Worksheet Printable Pdf Download

Simplify B2 3 B2 C2 3 C2 3 Divided By A B 3 B C 3 C Math Polynomials Meritnation Com

Abstract Algebra 12 1 Definition Of A Ring Youtube Dubai Khalifa

A Combinatorial Proof Of Dixon S Identity Mathematics Stack Exchange

Www Math Umass Edu Coughlan 411 Midterm Review Pdf

2

Q Tbn And9gcrswdldblxmiitn Ggstx6knbcgxw3sex0r673zeswoh Igfkvn Usqp Cau

2

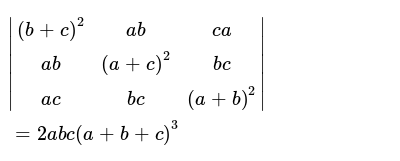
B C 2 Ab Ca Ab A C 2 Ac A B 2 2abc A B C 3

Search Q A 5e3 2bb 5e3 2bc 5e3 Formula Tbm Isch

Http Oregonstate Edu Instruct Mth341 Garity Fall00 Section1 4 Pdf

Mualphatheta Org Upload Files Pdf Titufall06 Pdf

Prove The Triple Scalar Product Identity A Btimes C Atimes B C Holooly Com

2

A3 C3 Formula

Special Identities A3 C3 3abc Youtube

Ng By Using A Suitable Identity B A B 3 B C 3 C A

3 What Does This Asterisk Mean And Why Is The Answer B Sat

2

A B C 3 Identity

2

2

Special Identity A3 C3 3abc Youtube

Cubic Identities Intro Ppt Download

What Are The Value Of B And C For Which The Identity Math F X 1 F X 8x 3 Math Is Satisfied Where Math F X Bx 2 Cx D Math Quora

Http Math Msu Edu Chamatth Teaching 310summer18 Hw3 Sol Pdf

The Identity Of Neomycin A 1 Neamine 2 And The Methanolysis Product Of Neomycin B And C 3 Pdf Document

Cubic Identities Ppt Download

Factorize 3 A B B C C A Identity A3 C3 3abc Pls Help Me This Brainly In

Find The Value Of A3 C3 3abc If A B C 15 And Ab Ca 74 Brainly In

2

Solved Problem 3 Vector Identities Use Index Notation To Chegg Com

Www Utdallas Edu Sxe0600 Solhw Pdf

Language English In Search Of The Samnites Adornment And Identity In Archaic Central Italy 750 350 B C

Cseweb Ucsd Edu Classes Sp09 Cse140 Mid1samp Sol Pdf

Solved Problem 3 Vector Identities Use Index Notation To Chegg Com

What Are Various Forms To Write A B C A Whole Cube Quora

2

Math Formulas Algebra Civil Service Exam Online Review Facebook

A B C 3 Identity

3 1 Y 14 Find The U 4 A B C 9 And Ab

Math Regents

Pdf Examining College Students Multiple Social Identities Of Gender Race And Socioeconomic Status Implications For Intergroup And Social Justice Attitudes

Question 9 Write Whether The Following Statements Are True Or False Justify Your Answer 1 Point

C3 Trig Identity Explanation Help The Student Room

Pdf A Remarkable Identity Found In Ramanujan S Third Notebook

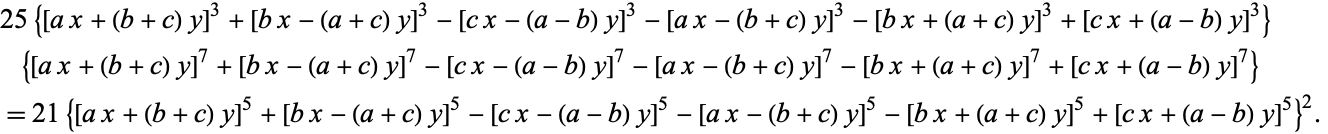
Hirschhorn 3 7 5 Identity From Wolfram Mathworld

Sectiongroups

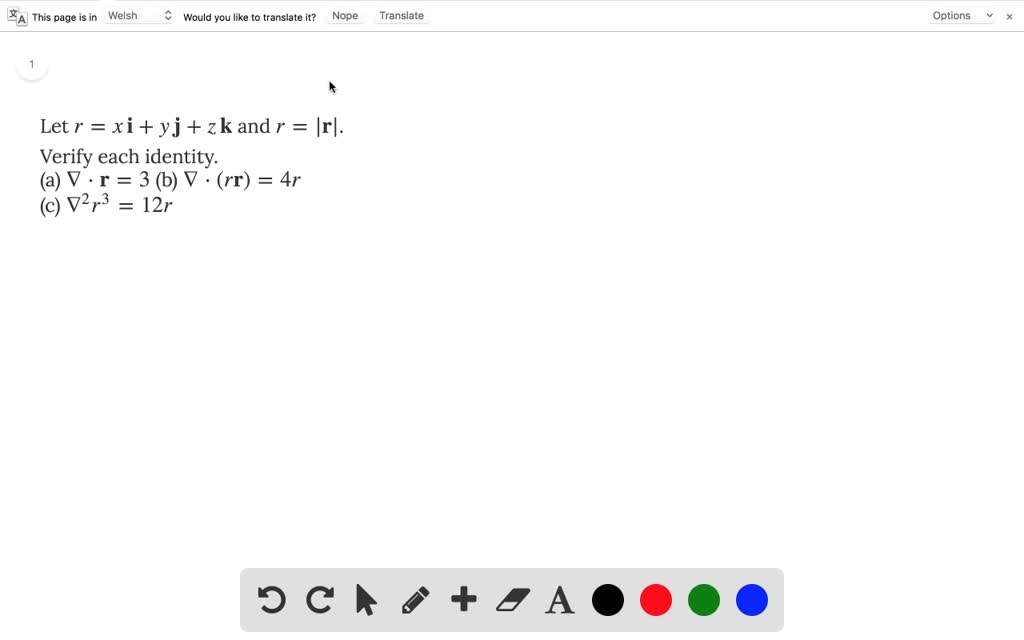
Solved Let R X Textbf I Y Textbf J

Identities Math Methods Learning Mathematics Math Formula Chart

New Page 1

Answered 8 12 Let R Be A Ring With Identity Bartleby

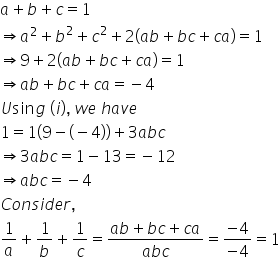
A B C 1 A B C 9 A B C 1 Then 1 A 1 B 1 C Mathematics Topperlearning Com 5m5fkjrr

V14 N1 Space Teaching Mathematics

2

If A B C 5 And Ab Ca 10 Prove A 3 B 3 C 3 3abc 25 Cbse Class 9 Maths Learn Cbse Forum

What Are Various Forms To Write A B C A Whole Cube Quora

2

Ocw Mit Edu Courses Physics 8 05 Quantum Physics Ii Fall 13 Assignments Mit8 05f13 Ps4 Pdf

Inequalities From The Word 1995 05

Factorize The Following By Using Suitable Identity A B 3 B C 3 C A 3 Brainly In

Algebraic Identity A B C 3 Schoolserve In

Incoming Term: (a+b+c)^3 identity, a^3+b^3+c^3-3abc identity, what is the identity of (a+b)3,